martes, 29 de septiembre de 2015

ELASTICIDAD
 
 La elasticidad, es una propiedad mecánica de los sistemas, decimos que un material es elástico cuando al aplicarle una fuerza, se deforma, y, al dejar de aplicar la fuerza, vuelve a su forma original.

Los materiales que al ser deformados y dejar de aplicar la fuerza, no vuelven a su forma original, se llaman inelásticos o plásticos.

Son materiales elásticos, un resorte, una gomita elástica, la piel, los músculos, entre otros.

Materiales plásticos, son por ejemplo un chicle, plasticina, cemento...


Todos los materiales elásticos tienen un límite de elasticidad, lo cual significa que si aplicamos una fuerza mayor al límite de elasticidad, el material queda deformado o se rompe.

Las partículas se mantienen unidas por fuerzas de atracción entre ellas, las que hacen que al separarlas vuelvan a su lugar, pero si las separamos demasiado, éstas fuerzas no son suficientes para volver a unirlas. El límite elasticidad depende de cada material.
 
 
 
 
La elasticidad es estudiada por la teoría de la elasticidad, que a su vez es parte de la mecánica de sólidos deformables. La teoría de la elasticidad (TE) como la mecánica de sólidos (MS) deformables describe cómo un sólido (o fluido totalmente confinado) se mueve y deforma como respuesta a fuerzas exteriores. 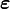La diferencia entre la TE y la MS es que la primera solo trata sólidos en que las deformaciones son termodinámicamente reversibles y en los que el estado tensiones \boldsymbol{\sigma} en un punto \mathbf{x} en un instante dado dependen solo de las deformaciones \boldsymbol{\varepsilon} en el mismo punto y no de las deformaciones anteriores (ni el valor de otras magnitudes en un instante anterior). Para un sólido elástico la ecuación constitutiva funcionalmente es de la forma:
\boldsymbol{\sigma}(\mathbf{x},t) = \hat{T}(\boldsymbol{\varepsilon}(\mathbf{x},t);\mathbf{x}), \qquad \qquad \hat{T}:\mathcal{T}_2(\R^3) \times \R^3 \to \mathcal{T}_2(\R^3)
donde \scriptstyle \mathcal{T}_2(\R^3) denota el conjunto de tensores simétricos de segundo orden del espacio euclídeo. Si el sólido es homogéneo el valor de la función anterior no dependerá del segundo argumento.
La propiedad elástica de los materiales está relacionada, como se ha mencionado, con la capacidad de un sólido de sufrir transformaciones termodinámicas reversibles e independencia de la velocidad de deformación (los sólidos viscoelásticos y los fluidos, por ejemplo, presentan tensiones dependientes de la velocidad de deformación). Cuando sobre un sólido deformable actúan fuerzas exteriores y éste se deforma se produce un trabajo de estas fuerzas que se almacena en el cuerpo en forma de energía potencial elástica y por tanto se producirá un aumento de la energía interna. El sólido se comportará elásticamente si este incremento de energía puede realizarse de forma reversible, en este caso se dice que el sólido es elástico.
 
ELASTICIDAD LINEAL:
Un caso particular de sólido elástico se presenta cuando las tensiones y las deformaciones están relacionadas linealmente, mediante la siguiente ecuación constitutiva:
\sigma_{ij} = \sum_{k,l} C_{ijkl}\varepsilon_{kl} \,
Cuando eso sucede se dice que el sólido es elástico lineal. La teoría de la elasticidad lineal es el estudio de sólidos elásticos lineales sometidos a pequeñas deformaciones de tal manera que además los desplazamientos y deformaciones sean "lineales", es decir, que las componentes del campo de desplazamientos u sean muy aproximadamente una combinación lineal de las componentes del tensor deformación del sólido. En general un sólido elástico lineal sometido a grandes desplazamientos no cumplirá esta condición. Por tanto la teoría de la elasticidad lineal solo es aplicable a:
  • Sólidos elásticos lineales, en los que tensiones y deformaciones estén relacionadas linealmente (linealidad material).
  • Deformaciones pequeñas, es el caso en que deformaciones y desplazamientos están relacionados linealmente. En este caso puede usarse el tensor deformación lineal de Green-Lagrange para representar el estado de deformación de un sólido (linealidad geométrica).
Debido a los pequeños desplazamientos y deformaciones a los que son sometidos los cuerpos, se usan las siguientes simplificaciones y aproximaciones para sistemas estables:
  • Las tensiones se relacionan con las superficies no deformadas
  • Las condiciones de equilibrio se presentan para el sistema no deformado
Para determinar la estabilidad de un sistema hay presentar las condiciones de equilibrio para el sistema deformado.

Tensión[editar]

Componentes del tensor tensión en un punto P de un sólido deformable.
La tensión en un punto se define como el límite de la fuerza aplicada sobre una pequeña región sobre un plano π que contenga al punto dividida del área de la región, es decir, la tensión es la fuerza aplicada por unidad de superficie y depende del punto elegido, del estado tensional de sólido y de la orientación del plano escogido para calcular el límite. Puede probarse que la normal al plano escogido nπ y la tensión tπ en un punto están relacionadas por:
{t_\pi} = {\mathbf{T}(n_\pi)} \,
Donde T es el llamado tensor tensión, también llamado tensor de tensiones, que fijada una base vectorial ortogonal viene representado por una matriz simétrica 3x3:
\mathbf{T} = \left( \begin{matrix} \sigma_{xx} & \sigma_{xy} & \sigma_{xz}\\ \sigma_{yx} & \sigma_{yy} & \sigma_{yz}\\ \sigma_{zx} & \sigma_{zy} & \sigma_{zz} \end{matrix} \right) = \left( \begin{matrix} \sigma_x & \tau_{xy} & \tau_{xz}\\ \tau_{yx} & \sigma_y & \tau_{yz}\\ \tau_{zx} & \tau_{zy} & \sigma_z \end{matrix} \right)
Donde la primera matriz es la forma común de escribir el tensor tensión en física y la segunda forma usa las convenciones comunes en ingeniería. Dada una región en forma de ortoedro con caras paralelas a los ejes coordenados situado en el interior un sólido elástico tensionado las componentes σxx, σyy y σzz dan cuenta de cambios de longitud en las tres direcciones, pero que no distorsinan los ángulos del ortoedro, mientras que las componentes σxy, σyz y σzx están relacionadas con la distorsión angular que convertiría el ortoedro en un paralelepípedo.

Deformación

En teoría lineal de la elasticidad dada la pequeñez de las deformaciones es una condición necesaria para poder asegurar que existe una relación lineal entre los desplazamientos y la deformación. Bajo esas condiciones la deformación puede representarse adecuadamente mediante el tensor deformación infinitesimal o tensor de pequeñas deformaciones (este tensor solo es válido para algunas situaciones, siendo este un caso particular de los tensores de Cauchy-Almansy y Green-Saint-Venant) que viene dada por:
\mathbf{D} = \begin{pmatrix} \varepsilon_{xx} & \varepsilon_{xy} & \varepsilon_{xz} \\ \varepsilon_{yx} & \varepsilon_{yy} & \varepsilon_{yz} \\ \varepsilon_{zx} & \varepsilon_{zy} & \varepsilon_{zz} \end{pmatrix} = \begin{pmatrix} \varepsilon_{xx} & \frac{1}{2}\gamma_{xy} & \frac{1}{2}\gamma_{xz} \\ \frac{1}{2}\gamma_{yx} & \varepsilon_{yy} & \frac{1}{2}\gamma_{yz} \\ \frac{1}{2}\gamma_{zx} & \frac{1}{2}\gamma_{zy} & \varepsilon_{zz} \end{pmatrix}
Los componentes de la diagonal principal contienen los alargamientos (dilataciones), mientras que el resto de los componentes del tensor son los medios desplazamientos. Las componentes están linealmente relacionadas con los desplazmientos mediante esta relación:
\varepsilon_{ij} = {1 \over 2} \left ({\part u_i \over \part x_j} + {\part u_j \over \part x_i}\right )

Publicado por en

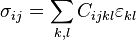
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)