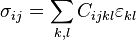En física y química se observa que, para cualquier sustancia o mezcla, modificando sus condiciones de temperatura o presión, pueden obtenerse distintos estados o fases, denominados
, en relación con las fuerzas de unión de las partículas (moléculas, átomos o iones) que la constituyen.
Todos los estados de agregación poseen propiedades y características diferentes; los más conocidos y observables cotidianamente son cuatro, llamados fases
. También son posibles otros estados que no se producen de forma natural en nuestro entorno, por ejemplo: condensado de Bose-Einstein, condensado fermiónico y estrellas de neutrones. Se cree que también son posibles otros, como el plasma de quark-gluón.
Los objetos en estado sólido se presentan como cuerpos de forma definida; sus átomos a menudo se entrelazan formando estructuras estrechas definidas, lo que les confiere la capacidad de soportar fuerzas sin deformación aparente. Son calificados generalmente como duros y resistentes, y en ellos las fuerzas de atracción son mayores que las de repulsión. En los sólidos cristalinos, la presencia de espacios intermoleculares pequeños da paso a la intervención de las fuerzas de enlace, que ubican a las celdillas en formas geométricas. En los amorfos o vítreos, por el contrario, las partículas que los constituyen carecen de una estructura ordenada.
Las sustancias en estado sólido suelen presentar algunas de las siguientes características:
Si se incrementa la temperatura de un sólido, este va perdiendo forma hasta desaparecer la estructura cristalina, alcanzando el estado líquido. Característica principal: la capacidad de fluir y adaptarse a la forma del recipiente que lo contiene. En este caso, aún existe cierta unión entre los átomos del cuerpo, aunque mucho menos intensa que en los sólidos. El estado líquido presenta las siguientes características:
Se denomina gas al estado de agregación de la materia que no tiene forma ni volumen definido. Su principal composición son moléculas no unidas, expandidas y con poca fuerza de atracción, haciendo que no tengan volumen y forma definida, provocando que este se expanda para ocupar todo el volumen del recipiente que la contiene, con respecto a los gases las fuerzas gravitatorias y de atracción entre partículas resultan insignificantes. Es considerado en algunos diccionarios como sinónimo de vapor, aunque no hay que confundir sus conceptos, ya que el término de vapor se refiere estrictamente para aquel gas que se puede condensar por presurización a temperatura constante. Los gases se expanden libremente hasta llenar el recipiente que los contiene, y su densidad es mucho menor que la de los líquidos y sólidos.
Dependiendo de sus contenidos de energía o de las fuerzas que actúan, la materia puede estar en un estado o en otro diferente: se ha hablado durante la historia, de un gas ideal o de un sólido cristalino perfecto, pero ambos son modelos límites ideales y, por tanto, no tienen existencia real.
En los gases reales no existe un desorden total y absoluto, aunque sí un desorden más o menos grande.
En un gas, las moléculas están en estado de caos y muestran poca respuesta a la gravedad. Se mueven tan rápidamente que se liberan unas de otras. Ocupan entonces un volumen mucho mayor que en los otros estados porque dejan espacios libres intermedios y están enormemente separadas unas de otras. Por eso es tan fácil comprimir un gas, lo que significa, en este caso, disminuir la distancia entre moléculas. El gas carece de forma y de volumen, porque se comprende que donde tenga espacio libre allí irán sus moléculas errantes y el gas se expandirá hasta llenar por completo cualquier recipiente.
Para cada elemento o compuesto químico existen determinadas condiciones de presión y temperatura a las que se producen los cambios de estado, debiendo interpretarse, cuando se hace referencia únicamente a la temperatura de cambio de estado, que ésta se refiere a la presión de la atm. (la presión atmosférica). De este modo, en "condiciones normales" (presión atmosférica, 0 °C) hay compuestos tanto en estado sólido como líquido y gaseoso (S, L y G).
Los procesos en los que una sustancia cambia de estado son: la sublimación (S-G), la vaporización (L-G), la condensación (G-L), la solidificación (L-S), la fusión (S-L), y la sublimación inversa (G-S). Es importante aclarar que estos cambios de estado tienen varios nombres.
ESTADOS DE AGREGACION
· Estado Gaseoso
Los gases difieren fundamentalmente de los líquidos y de los sólidos en que el
volumen depende de su T ° y de la P aplicada.
A bajas P y altas T °, se cumplen aproximadamente las leyes de Boyle, Gay Lussac y Avogadro, tal como se expresan en la ecuación de estado de los gases (Gas Ideal):
P.V = n.R.T
Pero a medida que aumenta la P o disminuye la T °, aparecen desviaciones manifiestas del comportamiento ideal. Esto se ve cuando el Factor de Compresibilidad (Z) se desvía de la unidad, sabiendo que dicho desvío se debe al comportamiento más real de un gas. Dicho Z se calcula como:
P.V/R.T = 1 (para un mol del gas).
NOTA: Las Fuerzas de atracción Intermoleculares hacen que el Z < 1, mientras que el efecto basado en el volumen de las moléculas hace que el Z > 1.
La ley de Boyle debe invalidarse a presiones muy elevadas, pues para tales presiones pronostica volúmenes de gases infinitesimalmente pequeños, que realmente no podrían existir pues el menor volumen que presentan es el de las moléculas del mismo gas.
Por otra parte, las Fuerzas Intermoleculares, pues éstas reducen a las fuerzas de colisión, con lo que la p ejercida en las paredes de los recipientes por el gas real, es menor.
- Ecuación de un Gas Real:
Una de las más difundidas es la ecuación de Van der Waals, que introduce unas correcciones a la ecuación de los gases:
Corrección de P → P real = P + n².a/V²
Corrección de V → V real = V - n.b
Donde a y b depende de cada gas.
Hay que decir que la corrección de P se debe a las fuerzas intermoleculares y la de volumen a los volúmenes moleculares, por lo tanto la ecuación de un gas Real quedará como:
(P + n².a).(V - n.b)/V² = n.R.T
A esta ecuación se la llama Ecuación de Van der Waals.
- Difusión y Efusión. Ley de Graham:
- Difusión = es el proceso de expansión a través del espacio por parte del gas.
- Efusión= es el proceso de pasaje a través de poros pequeños por parte del gas.
- Ley de Graham (aplicable a la Efusión de gases) =
"El tiempo que tarda un volumen de un gas para pasar a través de un orificio, es inversamente proporcional a su velocidad de efusión", o sea que matemáticamente será:
t
2/t
1 = M
2/M
1 = δ
2/ δ
1
de donde se puede definir a la velocidad de Efusión como:
v = V/t
Licuefacción de Gases:
En
a tenemos un gas a elevada T y V, y baja P. Si disminuimos el V a T = constante, el gas se compacta según la Ley de Boyle (P*V = constante) y observamos como aumenta la presión hasta
b.
A dicha presión (
b), al disminuir el V vemos que la P no varía, esto se debe a que comienzan a ejercerse fuerzas de atracción entre las moléculas. Esta presión se mantiene constante. Hasta
C donde todo el gas se convierte en liq. y la pendiente de la curva
CD evidencia la incompresibilidad de los mismos.
La porción de curva
AB denota la existencia de gas solamente; la
CD,líquido; en cambio en la porción
BC coexisten en equilibrio, gas y líquido,en donde la proporción de líquido a gas aumenta cuando diminuye el volumen (de
b a
C).
Si se repite la experiencia a mayores T °, vemos que la curva es análoga a la anterior, excepto que la porción horizontal, sobre la cual se efectúa la
Licuefacción, es más corta. La misma se reduce a un punto (
E), el cual es el límite por encima de la cual no se puede licuar un gas, es decir, que no existe el líquido por encima de esa
Tc (Temperatura crítica),Pc (Presión Crítica) y Vc (Volumen Crítico), cualquiera sea la presión aplicada. la curva que pasa por el punto
E se denomina
Isotérma Crítica.
Generalmente se utiliza el término vapor para definir a una sustancia gaseosa cuando su temperatura está por debajo del
valor crítico, por lo tanto un vapor puede ser licuado por efecto de la presión.
- Presión de Vapor:
Es la presión a la cual vapor y líquido coexisten en equilibrio (dentro del tramo
BC de la curva de Licuefacción de gases). Dicha presión aumenta al elevarse la T °, estableciéndose un límite en el
Punto Crítico.
- Ecuación de Clapeyron-Clausius:
D Pv/dT = Lv/T.(V vapor - V líquido)
Donde:
D Pv/dT representa la velocidad de variación de la P de vapor con la T °.
Lv : calor Latente de Vaporización (Δ Hv).
V vapor y V líquido: Volúmenes de Vapor y Líquido respectivamente.
T: Temperatura Absoluta.
Si integramos entre dos puntos, obtendremos:
Ln (pv
2/pv
1) = - Lv.(1/T
2 - 1/T
1)/R
pv = e - Lv/(R*T)
- Estado Líquido
Para todo gas hay una temperatura en particular a la cual las fuerzas intermoleculares toman suficiente intensidad como para que las moléculas condensen, formando un nuevo estado: el líquido.
- Características del Estado Líquido:
En los gases las moléculas se mueven rápidamente y en forma desordenada. En los sólidos, se mantienen juntas y en posiciones ordenadas. En cambio en los líquidos, es una forma intermedia entre ambos, las moléculas se mueven más lentamente que en los gases; pero las fuerzas intermoleculares las mantiene juntas dentro de un volumen definido. No obstante, la velocidad con que se mueven éstas, les impide formar un retículo cristalino (que sí se da en los sólidos),es por ello que un líquido retiene su volumen pero no su forma, es decir, que adquieren la forma del recipiente que los contiene.
Un cambio de P casi no altera a los líquidos, puesto que hay poco espacio entre sus moléculas; en cambio un aumento en la T °, modifica ligeramente su volumen, por lo que la densidad del líquido disminuye.
- Difusión:
Dos líquidos que son mutuamente solubles, se difundirán el uno en el otro al juntarlos. La velocidad de difusión dependerá de las densidades de los mismos pero siempre serán menores a la de los gases. Esto es debido a que las moléculas de los líquidos están relativamente juntas, por lo tanto una molécula de un líquido sufre muchos choques con las otras en un período dado, lo que alienta el proceso de difusión.
- Tensión Superficial:
Las moléculas superficiales están sometidas a fuerzas que las atraen hacia el interior de los líquidos. Es como si la superficie de los mismos estuviesen sometidos a una constante
tensión,parecido a cuando una piel estrecha esta recubriendo una superficie.
A este fenómeno se lo denomina
tensión superficial y es una de las causas por la cual los líquidos tienden a adoptar la forma geométrica más simple,o sea la esfera (es el caso de las gotas de líquido en caída libre).
La medición de dicha tensión superficial se realiza a través de la experiencia del "capilar", en donde se observa el escalamiento de una semiesfera de líquido retenida dentro de un tubo capilar, del cual debe conocerse su radio para lograr así obtener el
Coeficiente de Tensión Superficial (γ):
γ = ½.h.g.δ.r
Donde:
h: es la altura que ha ascendido la semi-burbúja.
δ: es la densidad del líquido.
r: es el radio del tubo capilar.
- Viscosidad:
Es la resistencia que presentan los líquidos al movimiento, o podría decirse también que forma parte de un rozamiento interno del mismo, pues es una propiedad que se opone al movimiento de capas adyacentes que se alojen dentro del seno del mismo.
Cuando un cuerpo de inserta dentro del seno de un líquido, la viscosidad hace que su velocidad no sea nula en su estadía dentro de él, sino que adquiere una v = constante cuando la fuerza de gravedad equilibra la fuerza que realiza la viscosidad para sacarlo del líquido.
Para los cálculos de viscosidad en diferentes líquidos normalmente se utiliza la Fórmula de Stokes, que para una esfera de radio "r" que cae a v = constante será:
v = 2.g.r².(δ ´- δ)/9. μ
Donde:
M : es el Coeficiente de Viscosidad del Líquido.
δ ´: es la densidad de la esfera.
δ : es la densidad del líquido.
NOTA: Generalmente sucede que la
δ ´>> δ por lo que la fórmula se ve reducida a:
v = 2.g.r².δ ´/9. μ
La medición de la viscosidad se realiza indirectamente a través de una medición de tiempos de caída de un mismo objeto dentro de dos sustancias: una de viscosidad conocida y otra que será la que averiguaremos por medio de la fórmula:
t = μ /δ → μ = t. δ
NOTA: La
Viscosidad Cinemática (v) es la relación que existe entre la Viscosidad Absoluta y la Densidad del Líquido:
v = μ/δ
La relación de la Viscosidad con la T °, viene dada exponencialmente a través de la fórmula:
μ = A.e E/(R*T)
donde vemos que la
viscosidad disminuye a medida que la T ° aumenta. También debemos decir que A y E son ctes. que dependen del líquido usado.
- Evaporación:
Las moléculas de un líquido tienen Energías Cinéticas que se distribuyen muy ampliamente y cuyo promedio queda determinado según la T °. Esta energía cambia cuando las moléculas chocan entre sí, o sea que pueden tener energías altas y bajas en cualquier momento. Es por ello que las moléculas ubicadas en la superficie de los líquidos poseen mayor Energía que el resto, es decir que escapan a las fuerzas de atracción de las otras moléculas, pudiendo así, escapar al exterior (transformandosé en estado gaseoso) mediante la ayuda de calor exterior. Este proceso de "escape" se lo denomina
Evaporación o Vaporización.
La energía que reciben éstas moléculas para escapar hacia el exterior se denomina
Calor o Entalpía de Vaporización. Al producirse este escape de moléculas, la energía media de las mismas que quedaron en el líquido baja, por lo que la temperatura del mismo disminuye. Al evaporarse los líquidos de un sistema abierto, el calor fluye desde el exterior hacia la sustancia, para mantener su T °. De esta forma continúa el proceso de evaporación del líquido, pues se inserta energía a las moléculas más superficiales, con lo que vuelven a escapar.
La
velocidad de evaporación de un líquido
aumenta cuando aumenta la T ° del mismo, pues existen mayor cantidad de moléculas con energía suficiente como para ubicarse cerca de la superficie y evaporarse.
NOTA: La evaporación de líquido continúa hasta la eliminación del mismo, pues no existe restricción hacia el gas evaporado del mismo.
- Presión de Vapor:
Al restringirse la vaporización de un líquido, hay que considerar el proceso inverso al mismo: La
condensación. Este proceso consiste en el pasaje de las moléculas evaporadas a su estado original, el líquido.
Cuando las velocidades de vaporización y de condensación son iguales (a una T ° = constante) se dice que el líquido está en equilibrio con su vapor, lo que significa que el vapor está
saturado y la presión que ejerce el vapor en dicho estado de equilibrio se denomina
Presión de Vapor (pv). Debe de notarse que a T ° = constante y siendo el mismo líquido, las pv son iguales a pesar de que los volúmenes de vapor y líquido sean diferentes. Esto demuestra que la pv sólo depende de la T °.
Cuando la
Pv es igual a la P externa , se forman burbujas en el interior del líquido. Este es el
Punto de Ebullición del mismo (allí la T ° del líquido se mantiene constante durante la ebullición del mismo). Si la
P externa = 1 atm, la T ° del líquido en ese instante es el
Punto de Ebullición Normal del mismo.
NOTA: Recordemos que según la ley de presiones parciales de Dalton, en un recipiente con vapor será:
P atmosférica = Pv + PH2O
- Estado Sólido
Aquí rigen las leyes de las estructuras cristalinas, con las cuales se interpreta las propiedades se los sistemas sólidos.
- Transiciones en Sólidos:
En el cero absoluto existen casi todas las sustancias como estructuras cristalinas, pero a medida que aumenta la T °, éstas estructuras comienzan a vibrar hasta que llegan a una T ° en donde se desarma la estructura y el sólido deja de serlo, para transformarse en líquido. A este proceso se lo conoce como
fusión.
Al proceso inverso, se lo denomina
Congelación. Las T
f y T
congelación son idénticas y a dichas T ° se hallan en equilibrio ambas fases (en este tramo la T ° se mantiene constante).
Por otra parte,
la energía calórica que se necesita para realizar estos procesos se denomina
Calor de Fusión (o
de Congelación, según sea la conversión).
- Presión de Vapor en los Sólidos (Sublimación):
La curva que indica la variación de la Pv en función de la T °, para los sólidos, se denomina Curva de Sublimación. Esto se debe a que el pasaje desde el sólido hacia el vapor sin pasar por el líquido se lo denomina Sublimación.
Análogamente puede hacerse pasar al vapor hacia el sólido, por medio del enfriamiento del vapor, siempre que se cumpla que:
Pv < Pv sólido en la fusión.
El cambio de estado en la materia va acompañado por una absorción de calor, que será el Calor Latente de Sublimación (H
s), el cual viene relacionado con los calores de Fusión (H
f) y de Vaporización (H
v), siempre que estén referidos a la misma T °:
Hs = Hf + Hv
- Cristalografía:
Los sólidos pueden presentarse en forma amorfa o cristalina. En el caso de la primera, los átomos (o moléculas,o partículas) se ordenan de modo que la regularidad no prevalezca sobre las distancias considerables. Desde el punto de vista estructural, los sólidos amorfos se asemejan a los líquidos (ej.: vidrio, plásticos, etc.).
La forma cristalina, está dada por una sola longitud: La arista del cubo de la retícula formada. La estructura de cualquier sistema que corresponde a este retículo es la repetición en las tres direcciones de espacio de dicho elemento estructural. Estas estructuras se denominan cristalinas y los cuerpos que las poseen se llaman cristales.
Las redes están formadas por una consecutiva adyacencia de varias retículas cristalinas, de modo tal que cualquier punto de ella, puede ser usado como origen de un sistema.
- Elementos de Simetría:
- Plano de Simetría: es aquel que divide al cristal en dos partes iguales;
- Eje de Simetría: es aquel sobre el cual el cristal puede revolucionar de modo que presente más de una vez su imagen en su transcurso.
- Centro de Simetría: es aquel punto por el que puede pasar cualquier recta que se encuentre a la misma distancia en ambas direcciones.
- Redes de Bravais:
Se ha probado que solo son posibles 14 tipos de redes espaciales simples, es decir, que existen solo 14 maneras de distribuir puntos semejantes en el orden tridimensional.
- Grupo de Simetría:
Sólo hay 32 posibles combinaciones diferentes de los elementos de simetría de un cristal.
- Grupos Especiales:
Junto con las redes de Bravais, los 32 grupos de Simetría llevan 230 disposiciones diferentes que se denominan Grupos Especiales.
- Sistemas Cristalinos:
Las redes de Bravais y los Grupos de Simetría, pueden dividirse en 7 sistemas cristalinos que se diferencian por consideraciones de simetría. Algunos de ellos son:
- Cúbico.
- Tetragonal.
- Ortorrómbico.
- Hexagonal.
- Rombohédrico.
- Monoclinico.
- Triclínico.
NOTA: Los
Planos de Miller se utilizan para poder descubrir la forma en que se ordenan las moléculas en un cristal, a través del corte de dichos planos con las estructuras cristalinas. Sus
Indices están indicando la inversa de las intersecciones del plano con los ejes, siempre que sean números enteros.
- Imperfecciones de los Cristales:
-
Defecto de Frenkel: Al moverse una de las partículas del retículo, la estructura se mueve por completo, quedando corrida de su formación original.
-
Defecto de Schottky: la partícula desplazada deja el lugar vacío, que es ocupada por otra partícula, con lo cual el corrimiento es de elementos y no de estructuras.
-
Impurezas: Cuando encontramos dentro de los cristales, elementos que no son propios del mismo.
NOTA: para poder saber que tipo de estructura posee un cristal deberemos recurrir a los Rayos X, debido a que el tamaño de dichas retículas es sólo comparable con las longitudes de ondas de dichos rayos. El proceso consiste la difracción de los Rayos X sobre los cristales del elemento, produciéndose una imagen que permite obtener una idea de cómo se sitúan las partículas en ese elemento.
 es un vector unitario y normal a la superficie en el punto donde se pretende medir la presión. La definición anterior puede escribirse también como:
es un vector unitario y normal a la superficie en el punto donde se pretende medir la presión. La definición anterior puede escribirse también como: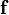 , es la fuerza por unidad de superficie.
, es la fuerza por unidad de superficie.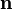 , es el vector normal a la superficie.
, es el vector normal a la superficie. , es el área total de la superficie S.
, es el área total de la superficie S.

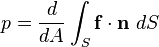


 en un punto
en un punto  en un instante dado dependen solo de las deformaciones
en un instante dado dependen solo de las deformaciones 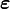 en el mismo punto y no de las deformaciones anteriores (ni el valor de otras magnitudes en un instante anterior). Para un sólido elástico la
en el mismo punto y no de las deformaciones anteriores (ni el valor de otras magnitudes en un instante anterior). Para un sólido elástico la 
 denota el conjunto de tensores simétricos de segundo orden del espacio euclídeo. Si el sólido es homogéneo el valor de la función anterior no dependerá del segundo argumento.
denota el conjunto de tensores simétricos de segundo orden del espacio euclídeo. Si el sólido es homogéneo el valor de la función anterior no dependerá del segundo argumento.